NSMQ 2023 Contest 5 Maths: Best Questions Review
What’s On This Page
Introduction
Another day is another chance. We have to keep moving forward. It is the fifth episode of our NSMQ Questions Review series and this time, it is all about the NSMQ 2023 Contest 5. If it is your first time here with us, please make sure to check our previous episodes out NSMQ Past Questions and Answers.
We know this contest took place around the same time as contest 4 and 6. What it means is that all the three had the same question sets from the round one (nsmq fundamentals) to the nsmq speed race to the nsmq problem of the day to the nsmq True or False to the nsmq riddles. If you have already gone through our previous episode, these questions won’t be new to you. Let’s begin the review.
Hi there,
If you are here, we are safe to assume you’ve a special interest in the NSMQ competition. Else if, you are preparing for WASSCE, SAT, ACT, AP,GSCE or any aptitude test. Else, you are a lover of Maths/Mathematics, Biology, Chemistry and Physics.
We have a proposal for you.
Get free access to our learning & training center to help with your development.
https://viewknust.com/nsmq/
NSMQ 2023 Contest 5
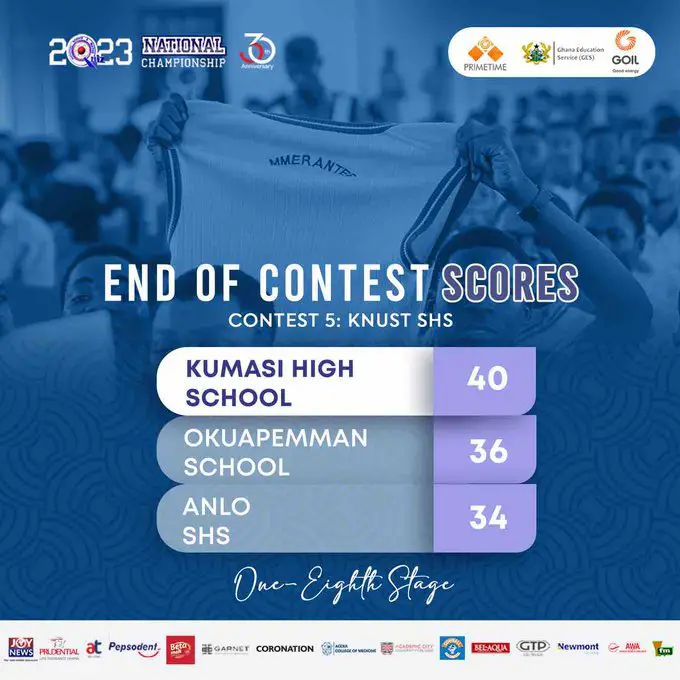
This was a one-eighth battle between Kumasi High School, Anlo SHS and Okuapemman School. The quest here is to take a look at the Maths/Mathematics questions that were asked. My focus will be on accuracy – how you can answer the questions right. I will dissect them in order of rounds: round one (nsmq fundamentals), nsmq speed race, nsmq problem of the day and nsmq True or False.
You can watch the particular contest NSMQ 2023 Contest 5 to see how the atmosphere, performance and reactions went.
Round One (NSMQ Fundamentals)
Set 1 – School A
Answer
Explanation
The question wants to test your understanding on trigonometry, specifically the trigonometric quadrants, and transformation.
Let’s first look at the transformation bit of the question
To understand everything here, I want to break it down into three parts.
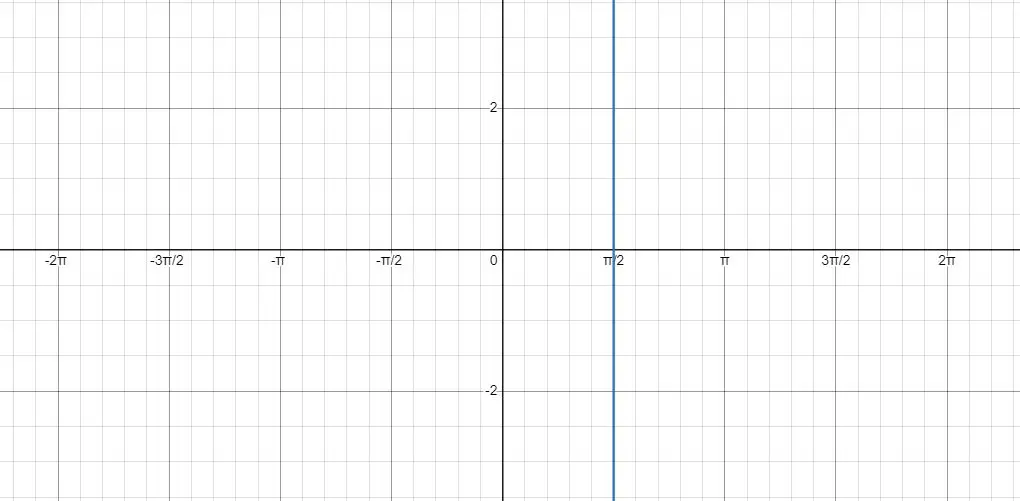
Below is the visual representation of the line on a graph.
Reflection means creating a mirror image of a point/line. We will need a mirror which will be the plane or axis of reflection. Just like looking into a mirror, the image will form on the other side of the mirror and at the same distance.
Now that we are good with the major part of the question, let’s move on to the unique aspect – the trigonometry
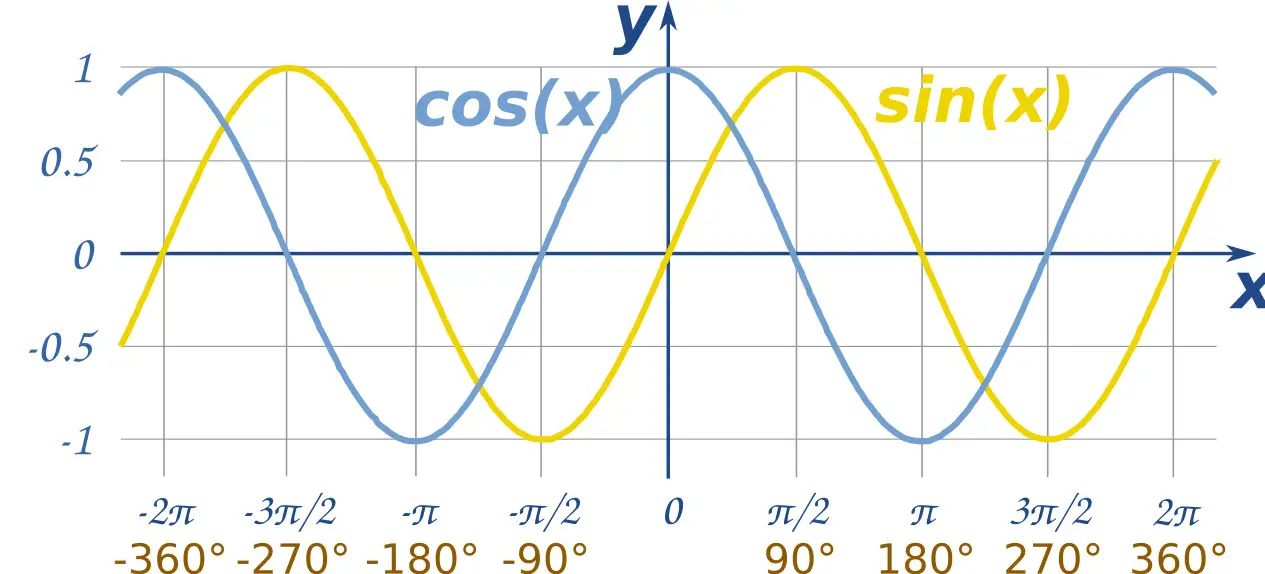
To reflect a trig. function, we should be well informed about the trig. quadrants because that is how we know what result to expect. Everything has been simplified on a picture, so I’ll use that to explain further.
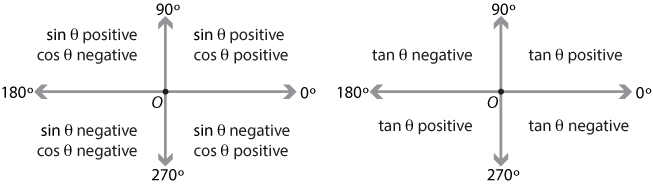
In the first diagram above, do not look at it like any other graph. It is drawn using the literal functions y=sin(theta) and y=cos(theta). We just use the theta for the axes to communicate effectively the sectioning of the quadrants.
To the main question now, let’s look at the sine graph.
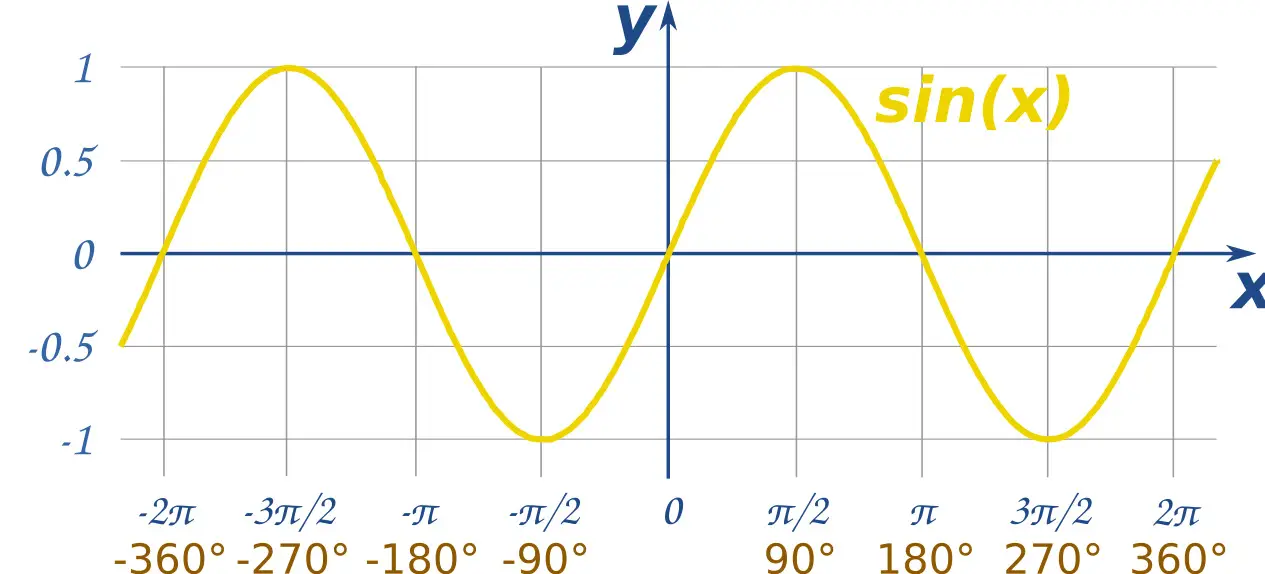
It is actually the positive side of this graph you see as the sections of the quadrant. Combining everything, you will see that any point on the sine curve when reflected fall on the same positive or negative side of the y-axis.
Take the part between pi/2 to the pi as a case study.
On the graph, their y is positive. When we reflect it about x=pi/2, the image falls between 0 and pi/2 which is still a positve y.
Same for the curve between pi and 3pi/2. The function is on the negative part of the y-axis. Reflect it and you will end up with the curve between 0 and -pi/2 which clearly is also at the negative side of the y-axis.
Take your time, look at the curve, read over again and you will understand the answer.
Set 1 – School B
Answer
Explanation
From where we left off with the previous question, this should be less challenging.
We can use the trigonometric quadrant to find the answer or we can use the cosine graph itself, depending on well you understand the concepts.
Using the trigonometric quadrant, we know we are reflecting in the line x=pi/2 or 90o.

Therefore, if the point is in the first quadrant, its image will be in the second quadrant. Likewise, a point in the second quadrant will have its image in the first quadrant. A point in the third quadrant will have the image in the fourth quadrant and a point in the fourth quadrant will have an image in the third quadrant.
Since cosine in the 1st quadrant is negated in the 2nd quadrant, you straightaway know the image will be y= -cosx. This is also confirmed by the fact that cosine is negative in the 3rd quadrant and positive in the 4th quadrant.
For those of us who cannot grasp the concept from the quadrants, we can take a look at the cosine graph.
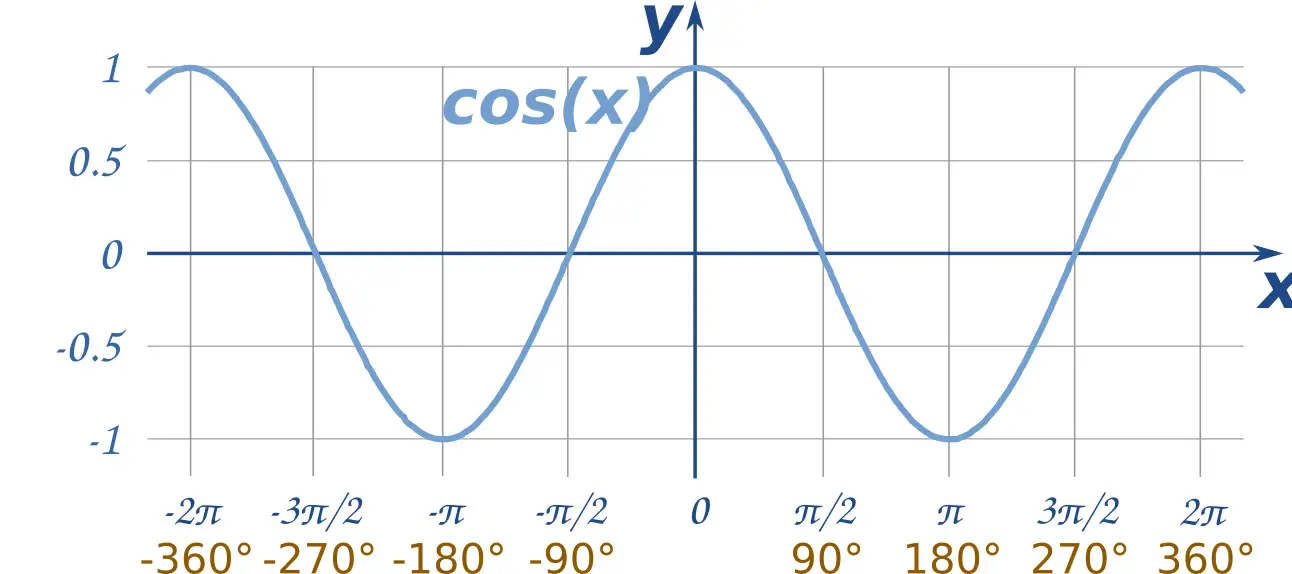
Take the curve between 0 and pi/2 as a case study. Since the curve is on the left of the mirror-line x=pi/2, our image will be on the right. Where? Between the pi/2 and the pi. Can you see what’s happening? Yeah, the image is on the negative side of y while the curve reflected was on the positive side of y.
Set 1 – School C
Answer
Explanation
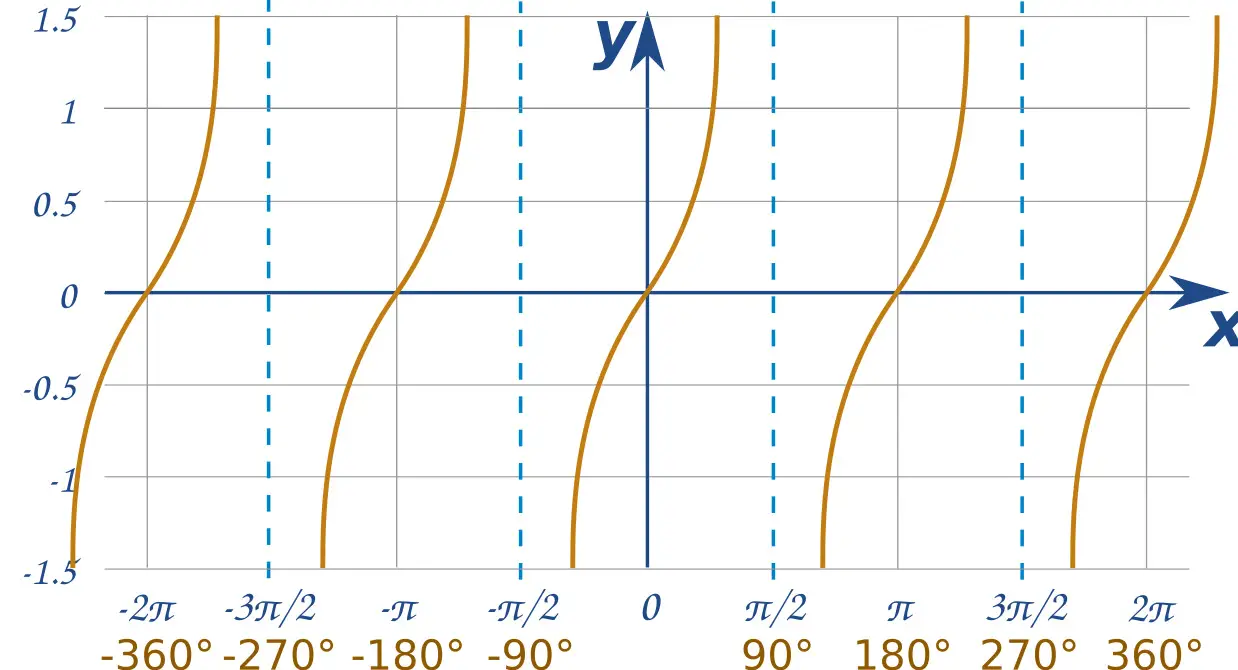
Here you can use the trig. quadrants, the tan gragh or play smart.
Since tan is sine over cosine, our reflected image should also be a reflected sine over a reflected cosine. We now know that a reflected sine is positive and a reflected cosine is negative, so positive over negative sure give us negative. Therefore, the equation for the image will be y= -tanx.
It is the same ideology from the above we see on the trig. quadrants.

While sine in the 1st quadrant reflect in the line x=pi/2 to the 2nd quadrant where it is still positive, cosine in the 1st quadrant reflect in x=pi/2 to the 2nd quadrant where it is negative. This implies that tan which is positve in the 1st quadrant will reflectin the line x=pi/2 to the 2nd quadrant and be negative. Same logic holds for the 3rd and 4th quadrant reflections in the line x=pi/2.
Set 2 – School A
Answer
Explanation
Set 2 – School B
Answer
Explanation
Set 2 – School C
Answer
Explanation
Round Two (NSMQ Speed Race)
Set 1 – First Question
Answer
Explanation
Set 1 – Second Question
Answer
Explanation
Set 1 – Third Question
Answer
Explanation
Round Three (NSMQ Problem Of The Day)
Question
Unfortunately, it was not a Math problem.
Round Four (NSMQ True or False)
Set 1 – School A
Answer
False
Explanation
The statement is not accurate. The negation of a statement is not always false. If the original statement is false, then the negation is true. If the original statement is true, then the negation is false. In logic, the negation simply asserts the opposite truth value of the original statement.
Set 1 – School B
Answer
False
Explanation
The converse of a statement being true doesn’t necessarily mean the original statement is true. The truth value of the converse is independent of the truth value of the original statement. For example, a statement could be true, but its converse might be either true or false.
Set 1 – School C
Answer
False
Explanation
The converse of a statement being false doesn’t necessarily mean the original statement is false. The truth value of the converse is independent of the truth value of the original statement. For example, a statement could be false, but its converse might be either true or false.
Set 2 – School A
Answer
False
Explanation
Set 2 – School B
Answer
False
Explanation
Set 2 – School C
Answer
True
Explanation
Conclusion
Do you feel like a better mathematician? Yeah, at least, you have either learnt new things or enforced old knowledge. It is my honor to have had this session with you. By going through these questions in the round one (nsmq fundamentals), the nsmq speed race, the nsmq Problem of the Day and the nsmq True or False, we get better each time.
I’ll be back with another episode and it will be on the NSMQ 2023 Contest 6. Until then, stay safe, stay sharp and stay practicing.